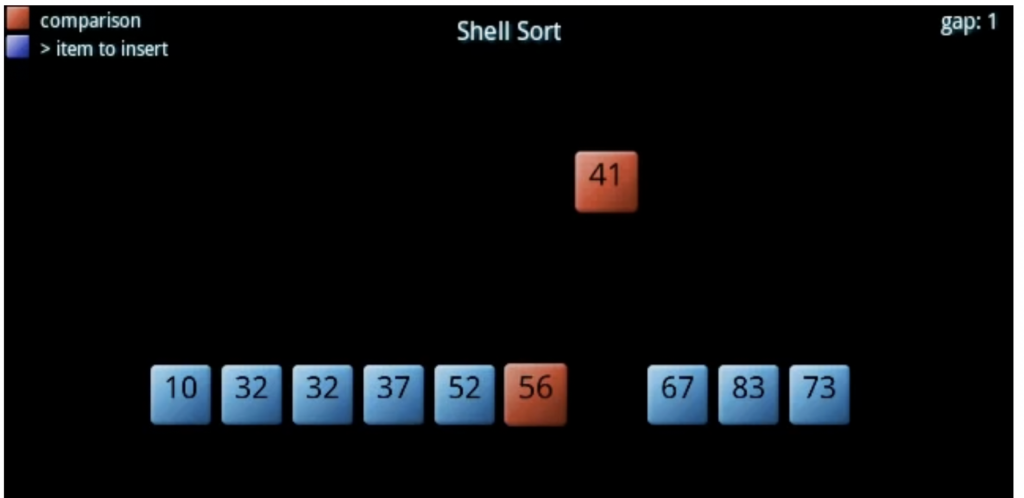
Shell Sort

Shell Sort is an in-place comparison-based sorting algorithm. It is an extension of the Insertion Sort algorithm that improves its efficiency by sorting elements that are far apart before sorting the adjacent elements. The algorithm was proposed by Donald Shell in 1959.

Here is the algorithm for Shell Sort:

1. Choose a gap sequence that determines the interval between elements being compared. The most commonly used sequence is the “Knuth’s sequence,” which is calculated using the formula: h = 3*h + 1, where h is the initial gap and is updated using the formula h = (h – 1) / 3.
2. Start with the largest gap and perform an insertion sort on the elements that are h positions apart.
3. Gradually reduce the gap size and repeat step 2 until the gap becomes 1.
4. Perform a final insertion sort with a gap of 1 to ensure the array is completely sorted.

The idea behind Shell Sort is to move elements towards their correct positions quickly by sorting elements that are far apart. This allows smaller elements to move towards the beginning of the array faster, reducing the total number of comparisons needed.

Shell Sort has the following characteristics:

• It is an in-place sorting algorithm, which means it operates on the input array itself without requiring additional memory.
• It is not a stable sorting algorithm, meaning that the relative order of equal elements may change during the sorting process.
• The time complexity of Shell Sort varies depending on the gap sequence used. The best-known sequence, the Knuth’s sequence, has an average-case time complexity of O(n^1.3) and a worst-case time complexity of O(n^2). However, there are other gap sequences that can improve the time complexity further.
• Shell Sort performs well for medium-sized arrays but may not be as efficient as some other sorting algorithms for very large datasets.

Overall, Shell Sort is a simple and efficient algorithm that provides a trade-off between simplicity and performance. It is particularly useful when a quick and easy-to-implement sorting algorithm is needed for medium-sized arrays.

The algorithm for Shell Sort is as follows:

1. Start with an array of elements to be sorted.
2. Define the gap sequence, which determines the interval between elements being compared. The most commonly used sequence is the Knuth’s sequence, calculated using the formula h = 3*h + 1, where h is the initial gap and is updated using the formula h = (h – 1) / 3.
3. Loop over the gap sequence in reverse order, starting from the largest gap.
4. For each gap value, perform an insertion sort on the subarrays that are h positions apart.
   • Starting from the first element at index h, compare it with the element at index 0 and swap if necessary.
   • Continue comparing and swapping elements that are h positions apart until reaching the end of the array.
   • Repeat this process for all subarrays in the main array.
5. Decrease the gap size and repeat step 4 until the gap becomes 1.
6. Finally, perform a regular insertion sort on the array with a gap of 1 to ensure the array is completely sorted.

Here is the pseudocode representation of the Shell Sort algorithm:

function shellSort(arr):
n = length(arr)
gap = 1

# Determine the initial gap using Knuth's sequence
while gap < n / 3:
    gap = 3 * gap + 1

# Perform shell sort with decreasing gap size
while gap > 0:
    for i = gap to n - 1:
        temp = arr[i]
        j = i

        # Shift elements that are h positions apart
        while j >= gap and arr[j - gap] > temp:
            arr[j] = arr[j - gap]
            j = j - gap

        arr[j] = temp

    gap = (gap - 1) / 3

return arr

This algorithm efficiently sorts the elements in the array by gradually reducing the gap size and performing insertion sort on subarrays. The choice of the gap sequence affects the algorithm’s efficiency, with the Knuth’s sequence being a commonly used and effective choice.

Application:

Shell Sort can be applied to sort arrays of any data type, making it a versatile sorting algorithm. It is particularly useful in scenarios where other efficient sorting algorithms like Quick Sort or Merge Sort may not be suitable due to their higher memory requirements or time complexity. Here are some applications where Shell Sort can be beneficial:

1. Small to Medium-Sized Arrays: Shell Sort performs well on small to medium-sized arrays, especially when the array is already partially sorted or has elements that are close to their final positions. It strikes a balance between simplicity and efficiency, making it a good choice for arrays that are not excessively large.
2. Embedded Systems: In resource-constrained environments such as embedded systems, where memory usage and processing power are limited, Shell Sort can be a suitable sorting algorithm due to its lower memory requirements compared to other sorting algorithms.
3. Offline Sorting: Shell Sort can be useful for offline sorting scenarios where the entire dataset is available at the beginning. Since Shell Sort performs well on partially sorted arrays, it can be advantageous when sorting data that is initially partially ordered or nearly sorted.
4. Educational Purposes: Shell Sort is often used as a teaching tool to introduce students to sorting algorithms. Its simple implementation and step-by-step refinement of sorting intervals help students understand the concept of incremental sorting and the impact of gap sequences on sorting efficiency.

It’s important to note that while Shell Sort has its advantages in specific scenarios, it may not be the most efficient algorithm for large arrays or datasets with specific patterns. In such cases, other sorting algorithms like Quick Sort, Merge Sort, or Heap Sort may provide better performance.

Complexity

The time complexity of Shell Sort depends on the gap sequence used. Let’s assume the worst-case time complexity when using the standard Shell’s gap sequence (dividing by 2):

• Best Case: O(n log n)
• Average Case: O(n^1.5)
• Worst Case: O(n^2)

The space complexity of Shell Sort is O(1) since it only requires a constant amount of additional space for swapping elements.

It’s worth noting that the actual time complexity of Shell Sort can vary depending on the implementation and the chosen gap sequence. There are alternative gap sequences that can yield better time complexities, such as the Sedgewick or Hibbard sequences. By using more sophisticated gap sequences, the average and worst-case time complexities of Shell Sort can be improved. However, these sequences may require more complex calculations and can increase the algorithm’s implementation complexity.

Example

def shell_sort(arr):
n = len(arr)
gap = n // 2

while gap > 0:
    for i in range(gap, n):
        temp = arr[i]
        j = i

        while j >= gap and arr[j - gap] > temp:
            arr[j] = arr[j - gap]
            j -= gap

        arr[j] = temp

    gap //= 2

return arr

Example usage:

arr = [9, 5, 1, 8, 3, 7, 2, 6, 4]
sorted_arr = shell_sort(arr)
print(sorted_arr)

In this example, the shell_sort function takes an array arr as input and performs the Shell Sort algorithm. It starts with a gap size of n // 2 and repeatedly divides the gap by 2 until it becomes 1. The algorithm then performs insertion sort on subarrays separated by the current gap size.

The while loop iterates over the array, comparing and swapping elements to sort them within each subarray. The inner while loop is responsible for the insertion sort process. Finally, the sorted array is returned.

When you run the code, it will output the sorted array [1, 2, 3, 4, 5, 6, 7, 8, 9].

About The Author