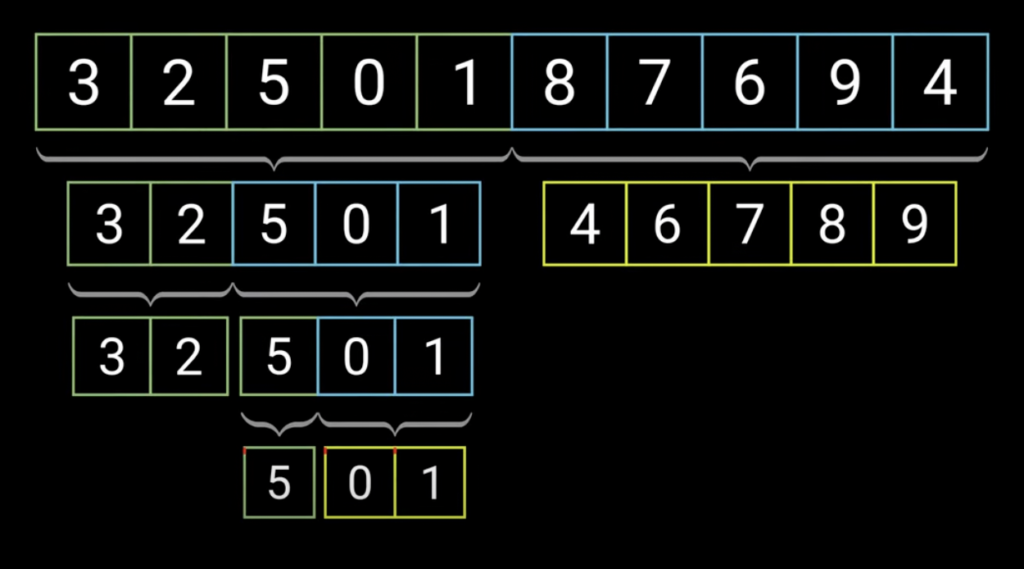
Merge Sort

Merge Sort is a divide-and-conquer sorting algorithm that divides the input array into smaller subarrays, sorts them recursively, and then merges them back together to obtain a sorted array. Here’s how Merge Sort works:

Divide: The input array is divided into two halves. This process continues recursively until the subarrays contain only one element or are empty.

Conquer: Once the subarrays have been divided to the smallest possible size, the merging process begins. Pairs of adjacent subarrays are merged by comparing the elements and placing them in the correct order.

Combine: The merging process is repeated, combining the merged subarrays into larger sorted subarrays until the entire array is sorted.

Here’s an example implementation of Merge Sort in Python:

def merge_sort(arr):
if len(arr) <= 1:
return arr

# Divide the array into two halves
mid = len(arr) // 2
left_half = arr[:mid]
right_half = arr[mid:]

# Recursively sort the subarrays
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)

# Merge the sorted subarrays
return merge(left_half, right_half)

def merge(left, right):
merged = []
i = j = 0

# Compare and merge the elements from the two subarrays
while i < len(left) and j < len(right):
    if left[i] < right[j]:
        merged.append(left[i])
        i += 1
    else:
        merged.append(right[j])
        j += 1

# Append the remaining elements, if any
merged.extend(left[i:])
merged.extend(right[j:])

return merged

Example usage

array = [7, 2, 4, 1, 5, 3]
sorted_array = merge_sort(array)
print(sorted_array)

In this code, the merge_sort function recursively divides the input array into smaller subarrays until the base case is reached (i.e., when the subarray has one element or is empty). The merge function is responsible for merging and sorting two subarrays.

The merge function compares the elements of the two subarrays and appends them to the merged list in the correct order. It uses two pointers (i and j) to keep track of the current positions in the left and right subarrays, respectively. After the elements from one subarray are exhausted, the remaining elements from the other subarray are appended to the merged list.

Finally, the sorted array is obtained by calling merge_sort on the input array, and it is printed as output: [1, 2, 3, 4, 5, 7].

Algorithm

The Merge Sort algorithm is a divide-and-conquer sorting algorithm that follows these steps:

Divide: Divide the unsorted list into two halves recursively until each sublist contains only one element. This is done by finding the middle index of the list and splitting it into two halves.

Conquer: Sort each sublist recursively by applying the merge sort algorithm to them. This step continues until each sublist contains only one element.

Merge: Merge the sorted sublists by repeatedly comparing the smallest elements of the sublists and placing them in order into a new sorted list. This is done by comparing the elements from the beginning of each sublist and appending the smaller element to the sorted list. The process continues until all elements are merged into a single sorted list.

The merge operation is the key step in Merge Sort. It involves comparing the elements from two sorted sublists and merging them into a single sorted sublist. The merging is done by iterating through the elements of both sublists, comparing the current elements, and adding the smaller element to the merged list. After one sublist is exhausted, the remaining elements from the other sublist are appended to the merged list.

The Merge Sort algorithm has a time complexity of O(n log n), where n is the number of elements in the input list. This makes it an efficient sorting algorithm for large lists. However, it requires additional space for creating temporary sublists during the sorting process.

Here is a high-level representation of the Merge Sort algorithm:

merge_sort(list):
if length of list is 1 or less:
return the list

Divide the list into two halves (left_half, right_half)
left_half = merge_sort(left_half)
right_half = merge_sort(right_half)
return merge(left_half, right_half)

merge(left_half, right_half):
Initialize an empty list (merged)
while left_half and right_half are not empty:
if first element of left_half <= first element of right_half:
append the first element of left_half to merged
remove the first element from left_half
else:
append the first element of right_half to merged
remove the first element from right_half

append the remaining elements of left_half to merged
append the remaining elements of right_half to merged
return merged

This algorithm can be implemented in various programming languages, including Python, Java, C++, and others, with slight differences in the syntax. The core idea remains the same, where the list is divided, sorted recursively, and merged back together to obtain the final sorted list.

Merge sort application.

The Merge Sort algorithm is widely used in various applications and scenarios where sorting is required. Some common applications of Merge Sort include:

1. General Sorting: Merge Sort is a general-purpose sorting algorithm that can be applied to sort any type of data. It is commonly used when a stable and efficient sorting method is needed.
2. External Sorting: Merge Sort is well-suited for sorting large datasets that do not fit entirely in the memory (RAM). It can efficiently handle sorting of data stored on external storage devices such as hard drives, where the data needs to be read and written in chunks.
3. Parallel Processing: Merge Sort can be easily parallelized, making it suitable for parallel and distributed computing environments. By dividing the sorting process into smaller subproblems and merging the results, Merge Sort can take advantage of multiple processors or machines to improve performance.
4. Online Streaming: Merge Sort can be used in scenarios where data is continuously arriving in a stream and needs to be sorted on-the-fly. As new elements are added to the stream, they can be merged with the existing sorted sequence, ensuring that the final output is always sorted.
5. Database Indexing: Merge Sort plays a crucial role in creating and maintaining indexes in databases. When creating an index, the data is often sorted to improve search and retrieval operations. Merge Sort is commonly used during the index-building process to efficiently sort and merge the data.
6. Inversion Count: Merge Sort can be used to determine the number of inversions in a list, which is the number of pairs of elements that are out of order. This information can be useful in various applications, such as analyzing the similarity between two datasets or detecting anomalies in data.

Overall, Merge Sort is a versatile sorting algorithm that finds applications in a wide range of fields, including data processing, database management, scientific computing, and more. Its stability, efficiency, and ability to handle large datasets make it a popular choice for many sorting requirements.

Complexity

The time complexity of the Merge Sort algorithm is O(n log n), where ‘n’ represents the number of elements to be sorted. This complexity makes Merge Sort one of the most efficient sorting algorithms, especially for large datasets.

The reason behind its efficient time complexity is the divide-and-conquer approach employed by Merge Sort. The algorithm divides the input array into two halves recursively until it reaches the base case of single elements. Then, it merges the smaller sorted arrays back together to form a sorted output.

The merge operation, which combines the two sorted subarrays, takes linear time proportional to the total number of elements being merged. Hence, the merging process contributes to the overall time complexity.

The space complexity of Merge Sort is O(n) because it requires additional space to store the temporary arrays during the merging process. In the worst case, when merging the smallest subarrays, the auxiliary space required is equal to the size of the input array.

One notable advantage of Merge Sort is its stability, meaning that the relative order of equal elements is preserved during sorting. This property is useful in scenarios where the original order of equal elements is significant.

Overall, Merge Sort’s time complexity of O(n log n) and stability make it a preferred choice in various applications where a stable and efficient sorting algorithm is required, especially for large datasets.

About The Author