Heap Sort

Heap Sort is an efficient comparison-based sorting algorithm that works by building a binary heap and repeatedly extracting the maximum (for ascending order) element from the heap. Here’s an explanation of the algorithm:

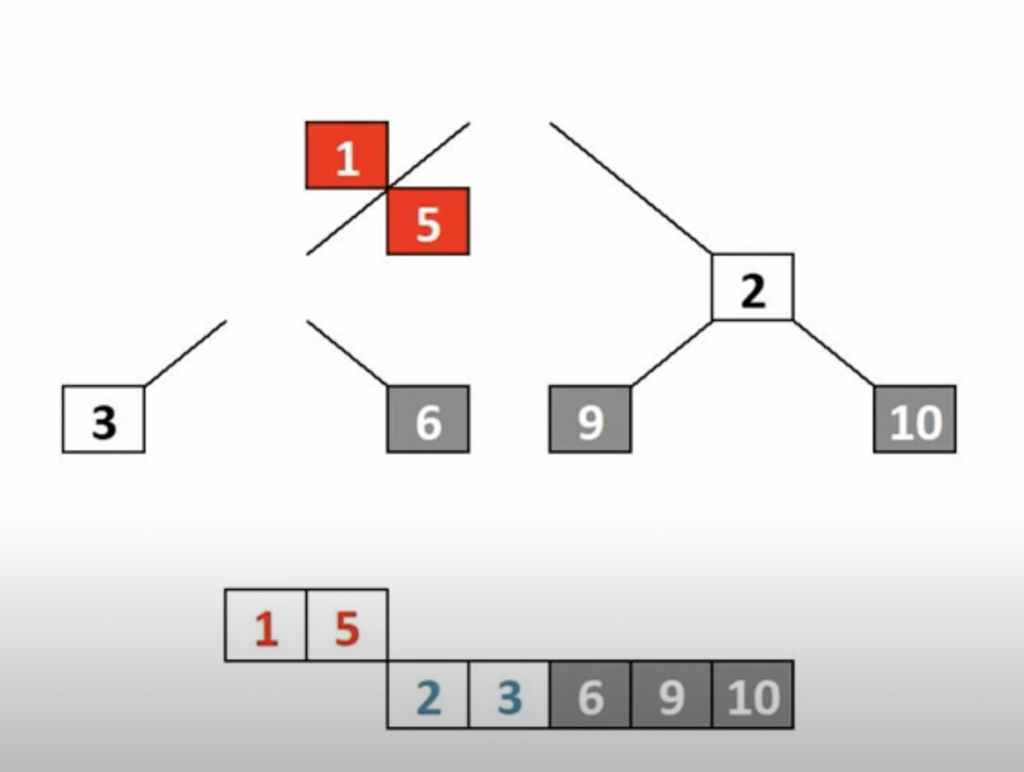
1. Build Max Heap: The first step of Heap Sort is to build a max heap from the given array. This is done by starting from the middle index of the array and performing the Max Heapify operation on each non-leaf node in a bottom-up manner. Max Heapify ensures that the parent node is greater than its child nodes.
2. Swap and Heapify: After building the max heap, the largest element (root of the heap) is at the top. We swap this element with the last element of the heap (last element of the array) and reduce the size of the heap by one. Then, we heapify the root element to maintain the max heap property.
3. Repeat: We repeat the swap and heapify process until the heap size becomes 1. At this point, the array is sorted in ascending order.

Here’s an example implementation of Heap Sort in Python:

def heapify(arr, n, i):
largest = i # Initialize largest as root
left = 2 * i + 1
right = 2 * i + 2

# Check if left child of root exists and is greater than the root
if left < n and arr[i] < arr[left]:
    largest = left

# Check if right child of root exists and is greater than the root
if right < n and arr[largest] < arr[right]:
    largest = right

# Swap the root if necessary
if largest != i:
    arr[i], arr[largest] = arr[largest], arr[i]
    heapify(arr, n, largest)

def heap_sort(arr):
n = len(arr)

# Build max heap
for i in range(n // 2 - 1, -1, -1):
    heapify(arr, n, i)

# Extract elements one by one
for i in range(n - 1, 0, -1):
    arr[i], arr[0] = arr[0], arr[i]  # Swap root with last element
    heapify(arr, i, 0)

return arr

Example usage

arr = [12, 11, 13, 5, 6, 7]
sorted_arr = heap_sort(arr)
print(sorted_arr)

In the above code, the heapify function is used to maintain the max heap property. It takes an array arr, the size of the heap n, and the index i as input. It compares the root element with its left and right child nodes, finds the largest element, and swaps it with the root if necessary. Then, it recursively calls itself on the affected sub-tree.

The heap_sort function starts by building a max heap from the given array. It iterates from the middle index to the first index and calls heapify on each node to build the max heap.

After building the max heap, it repeatedly swaps the root element (maximum) with the last element of the heap and reduces the size of the heap. It then calls heapify on the new root to restore the max heap property.

Finally, the function returns the sorted array.

The example usage demonstrates sorting an array [12, 11, 13, 5, 6, 7] using Heap Sort and printing the sorted result.

Algorithm

The algorithm for Heap Sort can be summarized as follows:

1. Build Max Heap: Build a max heap from the given array. This is done by starting from the middle index and moving up to the first index. For each index, perform the Max Heapify operation to ensure the max heap property is maintained.
2. Swap and Heapify: After building the max heap, the largest element (root of the heap) is at the top. Swap this element with the last element of the heap and reduce the size of the heap by one. Then, heapify the root element to maintain the max heap property. Repeat this step until all elements are sorted.

The detailed steps of the Heap Sort algorithm are as follows:

1. Initialize the array.
2. Build Max Heap:
   • Start from the middle index and move up to the first index.
   • For each index, perform the Max Heapify operation by comparing the node with its left and right child nodes.
   • Swap the node with the larger child if necessary.
   • Continue the process until all non-leaf nodes are heapified.
3. Swap and Heapify:
   • Set the heap size to the length of the array.
   • Repeat the following steps until the heap size becomes 1:
     • Swap the root element (largest element) with the last element of the heap.
     • Reduce the heap size by one.
     • Heapify the root element to maintain the max heap property.
4. The array is now sorted in ascending order.

The time complexity of Heap Sort is O(n log n) in all cases, where n is the number of elements in the array. The space complexity is O(1) since the sorting is done in-place without requiring additional memory.

It’s important to note that the algorithm can be implemented using either the iterative approach or the recursive approach. The code example provided earlier demonstrates the iterative approach.

Application:

Heap Sort has several applications in various fields. Some of the common applications include:

1. Sorting Algorithms: Heap Sort is often used as a sorting algorithm due to its efficient time complexity. It performs well on both small and large datasets, making it suitable for sorting applications in various domains.
2. Operating Systems: Heap Sort is used in operating systems for memory management. It helps in allocating and deallocating memory blocks efficiently by maintaining a priority queue of memory blocks based on their size.
3. Priority Queues: Heap Sort is used to implement priority queues, which are data structures where each element has a priority assigned to it. The elements with higher priority are dequeued before the elements with lower priority. Heap Sort’s ability to maintain the max heap property makes it suitable for implementing priority queues.
4. Graph Algorithms: Heap Sort is utilized in various graph algorithms, such as Dijkstra’s algorithm for finding the shortest path in a graph. It can efficiently extract the minimum element from a priority queue, which is required in many graph algorithms.
5. Order Statistics: Heap Sort can be used to find the kth smallest or largest element in an array efficiently. By building a max heap and repeatedly extracting the maximum element k times, the kth largest element can be found in O(n log k) time.
6. External Sorting: Heap Sort’s ability to work with limited memory makes it suitable for external sorting, where the dataset is larger than the available memory. It can be used to sort data stored on disk or in a database.

These are just a few examples of the applications of Heap Sort. Its efficient time complexity and suitability for various scenarios make it a valuable algorithm in the field of computer science and beyond.

The time and space complexity of Heap Sort can be described as follows:

Time Complexity:

Heap Sort has a time complexity of O(n log n) in all cases, where n is the number of elements in the array.

• Best-case complexity: O(n log n)
• Average-case complexity: O(n log n)
• Worst-case complexity: O(n log n)

Heap Sort has a time complexity of O(n log n) in all cases, where ‘n’ is the number of elements in the array to be sorted. This makes it an efficient sorting algorithm for both small and large datasets. The logarithmic factor arises from the process of building the heap and performing the heapify operation during the sorting process.

Space Complexity: Heap Sort has a space complexity of O(1) since it performs sorting in-place, without requiring additional memory proportional to the input size. The sorting is done by rearranging the elements within the given array itself, using the concept of a heap data structure.

Overall, Heap Sort is known for its efficient time complexity, especially in scenarios where a stable sorting algorithm is not a requirement. However, it does have a slightly higher constant factor compared to some other sorting algorithms due to the heapify operations.

About The Author