Bubble Sort

Bubble Sort is a simple sorting algorithm that works by repeatedly swapping adjacent elements if they are in the wrong order. It gets its name from the way smaller or larger elements “bubble” to their correct positions in each pass through the list.

Here’s how Bubble Sort works step-by-step with an example:

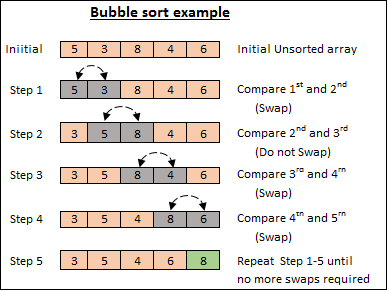
Suppose we have an unsorted list of integers: [5, 2, 8, 3, 1].

Start with the first element and compare it with the next element. If the next element is smaller, swap them. In our example, we compare 5 and 2. Since 2 is smaller, we swap them, resulting in [2, 5, 8, 3, 1].

Move to the next pair of elements (5 and 8) and compare them. Since they are already in the correct order, no swapping is required.

Repeat this process, moving to the next adjacent pairs and swapping if necessary, until you reach the end of the list. In our example, we compare 8 and 3, and then 8 and 1, resulting in [2, 5, 3, 1, 8].

At this point, the largest element (8) has “bubbled” to the end of the list. Since the largest element is now in its correct position, we can consider the sublist excluding the last element (8) as sorted.

Repeat steps 1-4 for the remaining unsorted sublist (excluding the last element) until the entire list is sorted.

After the first pass, the largest element (8) is in the correct position. In the second pass, we compare and swap elements until the second largest element is in its correct position, and so on.

Continue this process until no more swaps are required in a pass, indicating that the list is completely sorted.

Using Bubble Sort, the example list [5, 2, 8, 3, 1] would be sorted as follows:

Pass 1: [2, 5, 3, 1, 8]
Pass 2: [2, 3, 1, 5, 8]
Pass 3: [2, 1, 3, 5, 8]
Pass 4: [1, 2, 3, 5, 8]

In this case, it took four passes to sort the list completely. Bubble Sort has a worst-case time complexity of O(n^2), where n is the number of elements in the list. It is not very efficient for large lists but can be useful for small datasets or partially sorted lists.

// Original array
let array = [5, 2, 3, 1, 4];

// Bubble sort
for (let i = 0; i < array.length – 1; i++) {

for (let j = 0; j < array.length – i – 1; j++) {

if (array[j] > array[j + 1]) {
let temp = array[j];
array[j] = array[j + 1];
array[j + 1] = temp;
}
}
}

// Sorted array
console.log(array); // [1, 2, 3, 4, 5]

Bubble Sort Algorithm?

Bubble Sort is a simple comparison-based sorting algorithm. It repeatedly compares adjacent elements in an array and swaps them if they are in the wrong order. This process is repeated until the entire array is sorted. The algorithm gets its name from the way smaller elements “bubble” to the top of the array with each pass.

Here is the step-by-step description of the Bubble Sort algorithm:

1. Start with an unsorted array of elements.
2. Compare the first element with the second element. If the first element is greater than the second element, swap them.
3. Move to the next pair of adjacent elements (second and third), and continue comparing and swapping until the end of the array.
4. Repeat steps 2 and 3 for each element in the array, performing multiple passes.
5. After each pass, the largest element in the unsorted portion of the array “bubbles” up to its correct position at the end.
6. Repeat steps 2-5 until the entire array is sorted.

Here is the Python implementation of the Bubble Sort algorithm:

pythonCopy codedef bubble_sort(arr):
    n = len(arr)
    
    # Traverse through all array elements
    for i in range(n):
        
        # Last i elements are already in place
        for j in range(0, n-i-1):
            
            # Compare adjacent elements
            if arr[j] > arr[j+1]:
                # Swap elements if they are in the wrong order
                arr[j], arr[j+1] = arr[j+1], arr[j]

In this code, the outer loop iterates from 0 to n-1, where n is the number of elements in the array. This loop controls the number of passes needed to sort the array. The inner loop iterates from 0 to n-i-1, where i is the current pass. This loop compares adjacent elements and swaps them if necessary.

After the completion of the outer loop, the array will be sorted in ascending order.

It’s important to note that Bubble Sort is not the most efficient sorting algorithm, especially for large arrays, as it has a time complexity of O(n^2). However, it is simple to understand and implement, making it useful for educational purposes or for sorting small datasets.

Bubble Sort Complexity?

The complexity of the Bubble Sort algorithm can be described in terms of time complexity and space complexity.

Time Complexity: The worst-case time complexity of Bubble Sort is O(n^2), where ‘n’ is the number of elements in the array. This means that in the worst-case scenario, where the array is sorted in descending order, Bubble Sort will compare and swap elements multiple times until the entire array is sorted. The number of comparisons and swaps required is proportional to the square of the number of elements in the array.

In the best-case scenario, where the array is already sorted, Bubble Sort will still perform n-1 comparisons in each pass, but no swaps will be required. Therefore, the best-case time complexity of Bubble Sort is O(n).

On average, Bubble Sort also has a time complexity of O(n^2), making it an inefficient algorithm for large arrays. It is often outperformed by more efficient sorting algorithms such as Merge Sort or Quick Sort.

Space Complexity: The space complexity of Bubble Sort is O(1), which means that the additional space required by the algorithm does not depend on the size of the input array. Bubble Sort only requires a constant amount of extra space to store temporary variables used during comparisons and swaps.

It’s worth noting that Bubble Sort is an in-place sorting algorithm, meaning it does not require additional memory beyond the input array itself.

Overall, while Bubble Sort is simple to understand and implement, its time complexity makes it less suitable for sorting large arrays efficiently. It is commonly used for educational purposes or for sorting small datasets.

Bubble Sort Applications

Bubble Sort is a simple and intuitive sorting algorithm, but it is not commonly used in practice for large datasets due to its relatively slow performance compared to more efficient sorting algorithms. However, it can still have some practical applications in certain scenarios, such as:

1. Educational Purposes: Bubble Sort is often taught as an introductory sorting algorithm to help students understand the basic concepts of sorting. Its simplicity makes it a good starting point for learning about sorting algorithms.
2. Small Datasets: Bubble Sort can be useful for sorting small arrays or datasets with a limited number of elements. In such cases, the performance difference between Bubble Sort and more complex algorithms may not be significant, and the simplicity of Bubble Sort may outweigh its relatively slower speed.
3. Partially Sorted Arrays: If an array is partially sorted, meaning that only a few elements are out of order, Bubble Sort can perform well. This is because Bubble Sort’s adaptive nature allows it to take advantage of already sorted portions of the array and minimize unnecessary swaps.
4. Teaching and Testing Sorting Algorithms: Bubble Sort is often used as a benchmark or reference point when comparing the performance of other sorting algorithms. It provides a baseline for evaluating the efficiency and speed of more advanced sorting techniques.

Despite its limited practical applications, Bubble Sort’s simplicity and ease of implementation make it a valuable algorithm for educational purposes and for understanding the fundamentals of sorting.

About The Author